We humans generate 23 zettabytes of data every single day. I do not even know how many zeros are there in a Zetta. Yes, we are drowning in a sea of information. Then we hand over the data to the machines to make sense of it. They eventually do make sense of it, but we do not know how they do it(most of the time), especially when they work with high-dimensional data. For example, Images are data with dimensions equal to the product of its width and height. That’s huge!! However, We do have some hypotheses that can help in the explainability of these systems and one of them is the manifold hypothesis. I think it is a fascinating hypothesis worth discussing.
So what does it say?
The manifold hypothesis posits that many high-dimensional data sets that occur in the real world actually lie along low-dimensional latent manifolds inside that high-dimensional spa
https://en.wikipedia.org/wiki/Manifold_hypothesis
Too many things to unpack. Let’s Go!
Suppose I have a map of a city and want to pinpoint the location of a place. The location of a place is three-dimensional in a true sense, that is it can be described by the longitude, the latitude, and the altitude of the place. (Three variables)
However, you might have guessed it, we do not need the altitude of a place to go to a place, we just need the longitude and latitude of the place. This is one less variable than before. The problem is cut down to two dimensions from three dimensions. Less dimensions, we are happy, the machine is happy.
Latent Manifold
In machine learning, when we say “manifold,” we’re not necessarily talking about the strict mathematical definition. Instead, we use it in a more flexible way to describe a group of connected points.
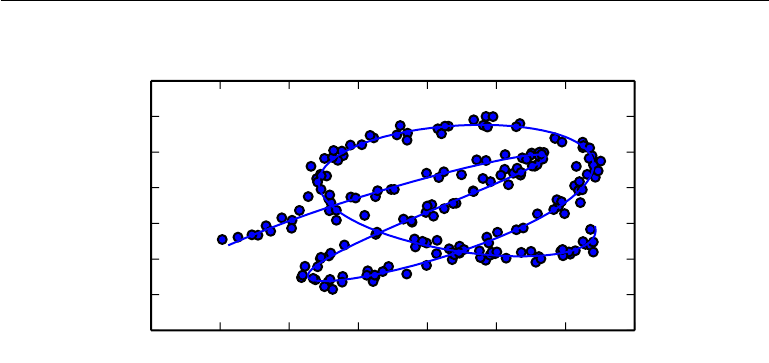
The above is two-dimensional data, the manifold here will be the line that connects the points. The algorithm must approximate this line.
The term latent means hidden, meaning we cannot observe the latent manifold directly, but it underlies the data we are observing.
In our map example, the latent manifold will be the two-dimensional data we cut down from three dimensions. It was latent (hidden) until we looked at the data from a certain perspective.
The manifold hypothesis thus says that most of the high-dimensional data in the real world can be approximated, with low-dimensional manifolds hidden inside the data. It’s like simplifying a complex idea by looking at only the most crucial parts.
Deep Learning
Deep learning algorithms are non-linear transformations of a given data in the simplest terms. The hypothesis is related to the effectiveness of these algorithms in learning these latent manifolds in high-dimensional data.
Our machine learning algorithm has to map usually a high-dimensional space to a lower-dimensional space. They learn these latent sub-manifolds, which are embedded in the data itself. (Remember the map example where two-dimensional space was embedded in three three-dimensional location data)
Inside one of these manifolds, you can smoothly transition between two inputs. In other words, you can seamlessly transform one into the other by following a continuous path where every point stays on the same track or pattern.
Being able to smoothly transition or interpolate between examples is a crucial aspect of deep learning. It means the system can learn from a few examples and apply that knowledge to new, similar situations. Imagine if you know how to do a few math problems and can smoothly tackle a new one that falls in between the ones you’ve already learned. That’s essentially the idea behind generalization in deep learning.
Model Architecture
Variational Autoencoders (VAE) and Generative Adversarial Networks (GAN) are two popular machine-learning techniques used to generate images. They learn to approximate an image manifold, which is a low-dimensional surface that contains all the possible images that can be generated by the model.
In simple terms, imagine that you have a dataset of images with many pixels. Each pixel is like a variable that describes the color of a small part of the image. If we plot all the images in this high-dimensional space, it would be difficult to see any patterns or structure in the data. However, the manifold hypothesis suggests that there is a low-dimensional surface that contains all the possible images that can be generated by the model. This surface is called the image manifold. The optimization task for these models is to learn to approximate this manifold. By doing so, the VAE and GAN can generate new images by extrapolating to newer data points along the image manifold.
VAEs are the backbone of the popular image generation model stable diffusion. It’s not magic, it’s math!
A cool thing would be to figure out how text is converted to images in these “latent” diffusion models.
Peace!



Leave a Reply